لاگرینج ضارب

ریاضیاتی کاملیت میں، طریقۂ لاگرینج ضارب (جو لاگرینج کے نام پر بولا جاتا ہے) کسی دالہ جو بندشوں کے زیر ہو کے عظمٰات اور صغیرات ڈھونڈنے کی ایک حکمت عملی فراہم کرتا ہے۔

Figure 1: Find x and y to maximize $f(x,y)$ subject to a constraint (shown in red) $g(x,y)=c$.

Figure 2: Contour map of Figure 1. The red line shows the constraint $g(x,y)=c$. The blue lines are contours of $f(x,y)$. The point where the red line tangentially touches a blue contour is our solution.

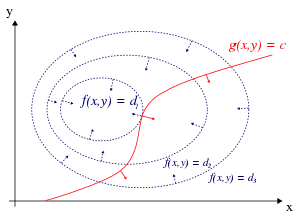
مثال کے طور پر (بائیں طرف شکل 1 دیکھو) کاملیت مسئلہ کو برتو، جس میں فنکشن $f(x,y)$ کی تکبیر کرنا ہے جبکہ بندش $g(x,y)=c$ کی بھی تسکین ہوتی ہو، یعنی

maximize $f(x,y)\,$

subject to $g(x,y)=c.\,$

اب ہم نیا متغیر ($\lambda$) متعارف کراتے ہیں، جسے لاگرینج ضارب کہتے ہیں اور اس لاگرینج فنکشن کا مطالعہ کرتے ہیں جو یوں تعریف ہے:

$\Lambda (x,y,\lambda )=f(x,y)+\lambda \cdot {\Big (}g(x,y)-c{\Big )}.$

اگر نقطہ $(x,y)$ اعظمی ہو اصل بندشی مسئلہ کا، تو پھر ایسا λ وجود رکھتا ہو گا کہ نقطہ $(x,y,\lambda )$ لاگرینج فنکشن Λ کا ساکن نقطہ ہو (ساکن نقاط وہ نقاط ہیں جہاں Λ کا جزوی مشتق صفر ہوں)۔ البتہ، تمام ساکن نقاط اصل مسئلہ کا حل نہیں دیتے۔ اس لیے، طریقۂ لاگرینج ضارب بندشی مسائل میں کاملیت کی لازم شرط ہے۔